Why do we grab an umbrella when the weather is set to be rainy for the day? How does your weather app recommend outdoor activities when the weather is sunny? It seems as simple as one plus one but these rules we use for our logical reasoning are the basis for many fields such as mathematics, computer science, philosophy, and legal reasoning.
What are the differences between inference rules and logical equivalence?
Inference rules are rules or guidelines that allow us to make a conclusion from valid premises.
For example:
P: It will rain | Q: I will get wet | P -> Q: If it rains, I will get wet
If P->Q and P is true, using Modus Ponens, one of the inference rules, we can assume that Q is also true. Then, we can assume that "I will get wet".
On the other hand, logical equivalence is the relationship between two logical statements that have the same truth values whatever the statements may be. Logical equivalence laws are only used to prove two statements that are logically the same, usually by simplifying the given expression of statements connected by logical operators [AND(∧), OR(∨), etc.]. They cannot be used to draw conclusions.
For example:
P: It will rain | Q: I will get wet | ~(P ∨ Q): It is not the case that it will rain or I will get wet
Using De Morgan's law the following statement: "It is not the case that it will rain or I will get wet (~(P ∨ Q))" is equivalent to "It won't rain and I won't get wet (~P ∧ ~Q)".
9 Fundamental Inference Rules:
There are 9 fundamental inference rules you can use to simplify statements, also known as premises or propositions to draw a conclusion. To make things easier to understand there is an example for all the rules. There is also a truth table to prove the rules which includes the variables, premises, and conclusion columns. When the premises and conclusion all have true value, the row is called a critical row. If there is a critical row, then you can say this argument is valid.
1. Modus Ponens
2. Modus Tollens
3. Hypothetical Syllogism
4. Conjunction
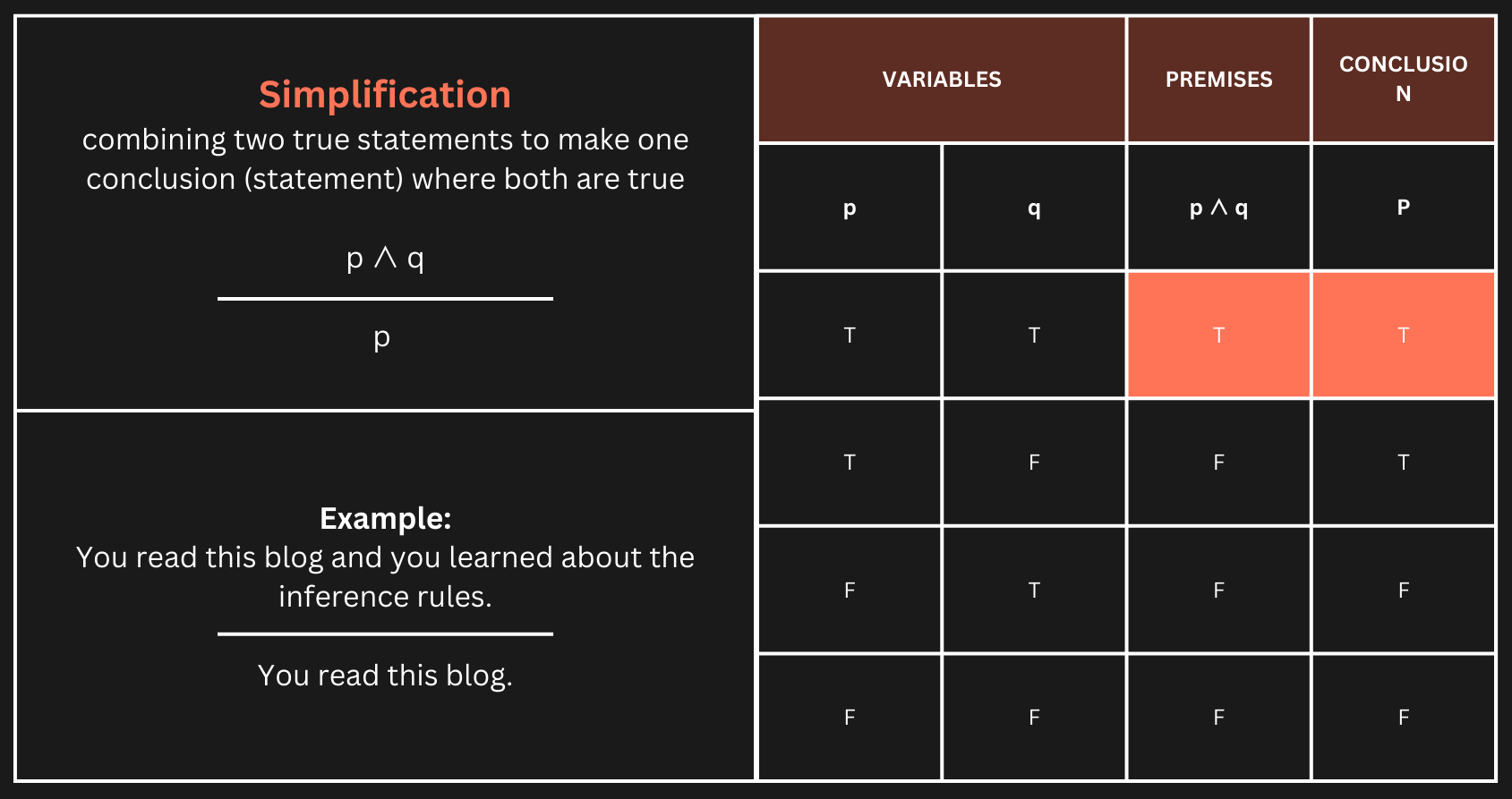
5. Simplification
6. Absorption
7. Addition
8. Disjunctive Syllogism
9. Constructive Dilemma
How do we use the inference rules?
Example problem #1:
In the back of an old cupboard, you discover a note signed
by a pirate famous for his bizarre sense of humor and
love of logical puzzles. In the note, he wrote that he had
hidden treasure somewhere on the property. He listed
five true statements (1-5 below) and challenged the
reader to use them to figure out the location of the
treasure.
1. If this house is next to a lake, then the treasure is not in
the kitchen.
2. If the tree in the front yard is an elm, then the treasure is
in the kitchen.
3. This house is next to a lake.
4. The tree in the front yard is an elm or the treasure is
buried under the flagpole.
5. If the tree in the backyard is an oak, then the treasure is
in the garage.
Epp, S. S. (2010). Discrete Mathematics with Applications (4th ed.). Brooks/Cole.p. 63, §2.3
Solution:
First, let's define our variables:
A: The house is next to a lake.
B: The treasure is not in the kitchen.
C: The tree in the front yard is an elm.
D: The treasure is buried under the flagpole.
E: The tree in the backyard is an oak.
F: The treasure is in the garage.
Then we can rewrite the premises as:
1. A -> ~B
2. C -> B
3. A
4. C V D
5. E -> F
Now using all the notations we can solve the problem.
(1) Using premises 1 and 3, and the Modus Ponens rule, we can simplify it as ~B
(2) Using 2 and (1), and the Modus Tollens rules, we can say ~C
(3) Finally, using (2) and 4, and Disjunctive Syllogism, we can conclude that the treasure is buried under the flagpole (D)
We bagged the treasure of the pirate using facts and logic🧠.
Example problem #2:
The famous detective Percule Hoirot was called in to solve
a baffling murder mystery. He determined the following
facts:
a. Lord Hazelton, the murdered man, was killed by a blow
on the head with a brass candlestick.
b. Either Lady Hazelton or a maid, Sara, was in the dining
room at the time of the murder.
c. If the cook was in the kitchen at the time of the murder,
then the butler killed Lord Hazelton with a fatal dose of
strychnine.
d. If Lady Hazelton was in the dining room at the time of
the murder, then the chauffeur killed Lord Hazelton.
e. If the cook was not in the kitchen at the time of the murder, then Sara was not in the dining room when the murder was committed.
f. If Sara was in the dining room at the time the murder was
committed, then the wine steward killed Lord Hazelton.
Is it possible for the detective to deduce the identity of
the murderer from these facts? If so, who murdered Lord
Hazelton? (Assume there was only one cause of death.)
Epp, S. S. (2010). Discrete Mathematics with Applications (4th ed.). Brooks/Cole.p. 63, §2.3
Solution:
First, let's define the variables:
A: Lord Hazelton, the murdered man, was killed by a blow on the head with a brass candlestick.
B: The maid, Sara, was in the dining room at the time of the murder.
C: Lady Hazelton was in the dining room at the time of the murder.
D: The butler killed Lord Hazelton with a fatal dose of strychnine.
E: The chauffeur killed Lord Hazelton.
F: The cook was in the kitchen at the time of the murder.
G: The wine steward killed Lord Hazelton.
Then, we will rewrite the premises:
a. A
b. B V C
c. F -> D
d. C -> E
e. ~F -> ~B
f. B -> G
Finally, we can draw the conclusion by the following steps:
1. From the contrapositive of c and e, and using hypothetical syllogism, we can see that ~D -> ~B.
Contrapositive of F -> D is ~D -> ~F
~D -> ~F
~F -> ~B
~D -> ~B
2. We know that since Lord Hazelton, the murdered man, was killed by a blow on the head with a brass candlestick, he cannot be killed using a fatal dose of strychnine. Therefore, D is false.
3. From 1 and 2, we know that ~B using Modus Ponens.
~D
~B
4. From statements 3 and b and the rule of Disjunctive Syllogism, we can say that C is true.
B V C
~B
C
5. Finally from d, we can see that E is true using Modus Ponens.
C -> E
C
E
We have solved that the culprit of the murder was the chauffeur using the inference rules we learned today. Hurray! 🎉
Thanks for making it to the end of the blog! You did it!😃 Here is a summary for you if you need it.

To learn more about Discrete Mathematics, you can read Discrete Mathematics with Applications by Susanna S. Epp.










Comments
Post a Comment